Project: cmaes

Lightweight Covariance Matrix Adaptation Evolution Strategy (CMA-ES) implementation for Python 3.

Project Details

Latest version: 0.10.0
Home Page
PyPI Page: https://pypi.org/project/cmaes/

Project Popularity

PageRank: 0.0015248169796761278
Number of downloads: 1373320

CMA-ES

Lightweight Covariance Matrix Adaptation Evolution Strategy (CMA-ES) [1] implementation.

visualize-six-hump-camel

News

2023/05/23 Our paper, M. Nomura, Y. Akimoto, and I. Ono, CMA-ES with Learning Rate Adaptation: Can CMA-ES with Default Population Size Solve Multimodal and Noisy Problems?, has been nominated for the Best Paper Award in the ENUM track at GECCO'23 :whale:
2023/04/01 Two papers have been accepted to GECCO'23 ENUM Track: (1) M. Nomura, Y. Akimoto, and I. Ono, CMA-ES with Learning Rate Adaptation: Can CMA-ES with Default Population Size Solve Multimodal and Noisy Problems?, and (2) Y. Watanabe, K. Uchida, R. Hamano, S. Saito, M. Nomura, and S. Shirakawa, (1+1)-CMA-ES with Margin for Discrete and Mixed-Integer Problems :tada:
2022/05/13 The paper, "CMA-ES with Margin: Lower-Bounding Marginal Probability for Mixed-Integer Black-Box Optimization" written by Hamano, Saito, @nomuramasahir0 (the maintainer of this library), and Shirakawa, has been nominated as best paper at GECCO'22 ENUM track.
2021/03/10 "Introduction to CMA-ES sampler" is published at Optuna Medium Blog. This article explains when and how to make the best use out of CMA-ES sampler. Please check it out!
2021/02/02 The paper "Warm Starting CMA-ES for Hyperparameter Optimization" written by @nomuramasahir0, the maintainer of this library, is accepted at AAAI 2021 :tada:
2020/07/29 Optuna's built-in CMA-ES sampler which uses this library under the hood is stabled at Optuna v2.0. Please check out the v2.0 release blog.

Installation

Supported Python versions are 3.7 or later.

$ pip install cmaes

Or you can install via conda-forge.

$ conda install -c conda-forge cmaes

Usage

This library provides an "ask-and-tell" style interface.

import numpy as np
from cmaes import CMA

def quadratic(x1, x2):
    return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2

if __name__ == "__main__":
    optimizer = CMA(mean=np.zeros(2), sigma=1.3)

    for generation in range(50):
        solutions = []
        for _ in range(optimizer.population_size):
            x = optimizer.ask()
            value = quadratic(x[0], x[1])
            solutions.append((x, value))
            print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
        optimizer.tell(solutions)

And you can use this library via Optuna [2], an automatic hyperparameter optimization framework. Optuna's built-in CMA-ES sampler which uses this library under the hood is available from v1.3.0 and stabled at v2.0.0. See the documentation or v2.0 release blog for more details.

import optuna

def objective(trial: optuna.Trial):
    x1 = trial.suggest_uniform("x1", -4, 4)
    x2 = trial.suggest_uniform("x2", -4, 4)
    return (x1 - 3) ** 2 + (10 * (x2 + 2)) ** 2

if __name__ == "__main__":
    sampler = optuna.samplers.CmaEsSampler()
    study = optuna.create_study(sampler=sampler)
    study.optimize(objective, n_trials=250)

CMA-ES variants

CMA-ES with Margin [3]

CMA-ES with Margin introduces a lower bound on the marginal probability associated with each discrete dimension so that samples can avoid being fixed to a single point. It can be applied to mixed spaces of continuous (float) and discrete (including integer and binary).

CMA-ES	CMA-ESwM

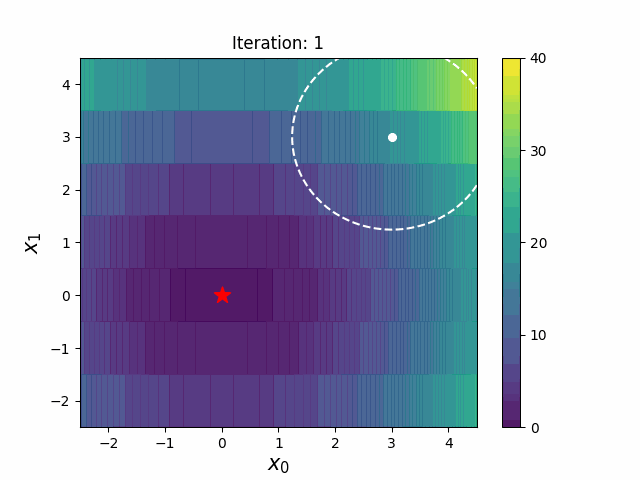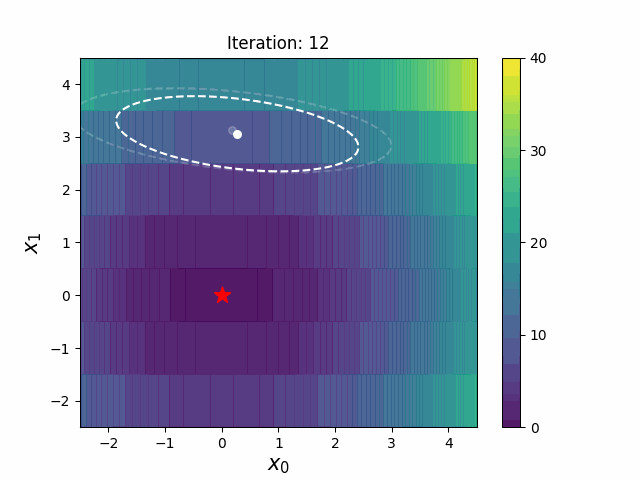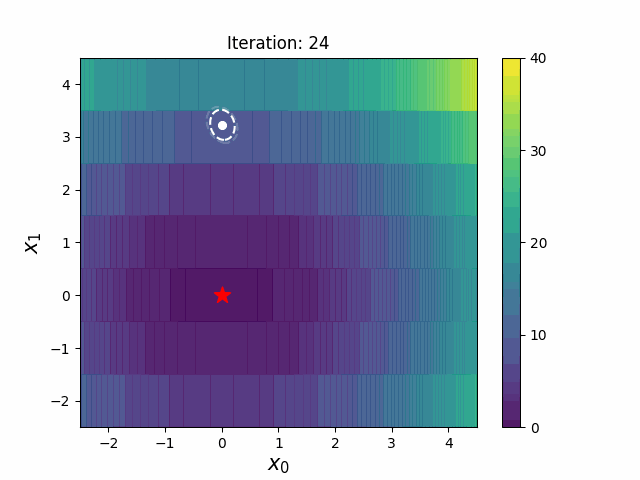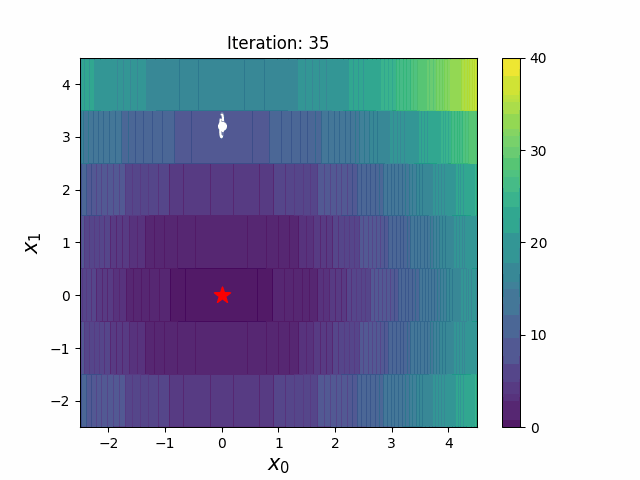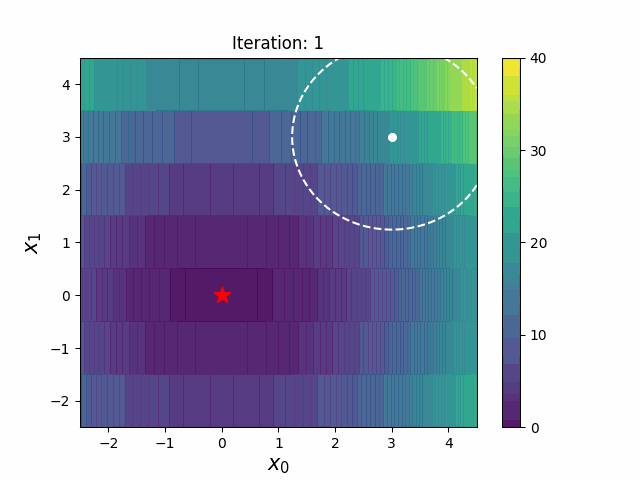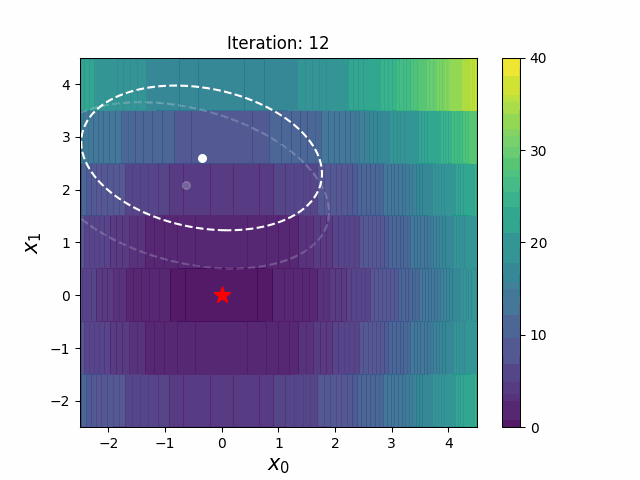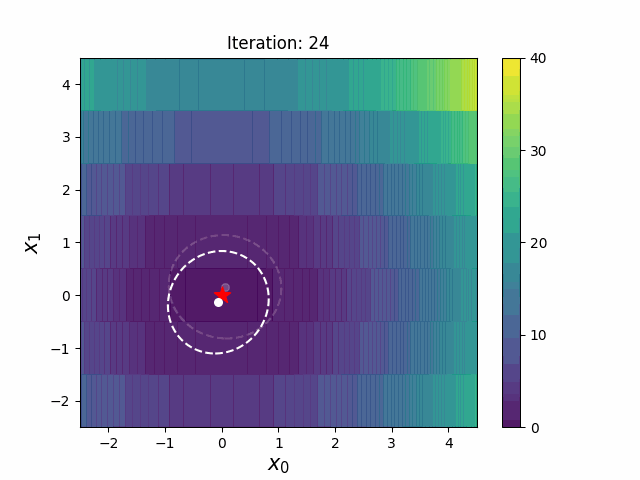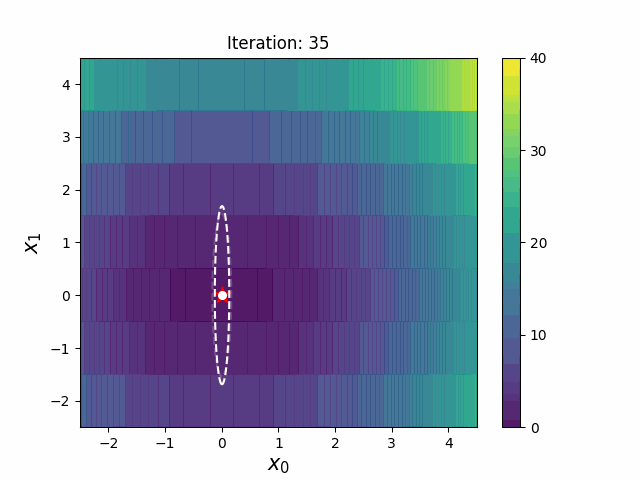The above figures are taken from EvoConJP/CMA-ES_with_Margin.

Source code

import numpy as np
from cmaes import CMAwM


def ellipsoid_onemax(x, n_zdim):
    n = len(x)
    n_rdim = n - n_zdim
    r = 10
    if len(x) < 2:
        raise ValueError("dimension must be greater one")
    ellipsoid = sum([(1000 ** (i / (n_rdim - 1)) * x[i]) ** 2 for i in range(n_rdim)])
    onemax = n_zdim - (0.0 < x[(n - n_zdim) :]).sum()
    return ellipsoid + r * onemax


def main():
    binary_dim, continuous_dim = 10, 10
    dim = binary_dim + continuous_dim
    bounds = np.concatenate(
        [
            np.tile([-np.inf, np.inf], (continuous_dim, 1)),
            np.tile([0, 1], (binary_dim, 1)),
        ]
    )
    steps = np.concatenate([np.zeros(continuous_dim), np.ones(binary_dim)])
    optimizer = CMAwM(mean=np.zeros(dim), sigma=2.0, bounds=bounds, steps=steps)
    print(" evals    f(x)")
    print("======  ==========")

    evals = 0
    while True:
        solutions = []
        for _ in range(optimizer.population_size):
            x_for_eval, x_for_tell = optimizer.ask()
            value = ellipsoid_onemax(x_for_eval, binary_dim)
            evals += 1
            solutions.append((x_for_tell, value))
            if evals % 300 == 0:
                print(f"{evals:5d}  {value:10.5f}")
        optimizer.tell(solutions)

        if optimizer.should_stop():
            break


if __name__ == "__main__":
    main()

Source code is also available here.

Warm Starting CMA-ES [4]

Warm Starting CMA-ES is a method to transfer prior knowledge on similar HPO tasks through the initialization of CMA-ES. Here is the result of an experiment that tuning LightGBM for Kaggle's Toxic Comment Classification Challenge data, a multilabel classification dataset. In this benchmark, we use 10% of a full dataset as the source task, and a full dataset as the target task. Please refer the paper and/or https://github.com/c-bata/benchmark-warm-starting-cmaes for more details of experiment settings.

benchmark-lightgbm-toxic

Source code

import numpy as np
from cmaes import CMA, get_warm_start_mgd

def source_task(x1: float, x2: float) -> float:
    b = 0.4
    return (x1 - b) ** 2 + (x2 - b) ** 2

def target_task(x1: float, x2: float) -> float:
    b = 0.6
    return (x1 - b) ** 2 + (x2 - b) ** 2

if __name__ == "__main__":
    # Generate solutions from a source task
    source_solutions = []
    for _ in range(1000):
        x = np.random.random(2)
        value = source_task(x[0], x[1])
        source_solutions.append((x, value))

    # Estimate a promising distribution of the source task,
    # then generate parameters of the multivariate gaussian distribution.
    ws_mean, ws_sigma, ws_cov = get_warm_start_mgd(
        source_solutions, gamma=0.1, alpha=0.1
    )
    optimizer = CMA(mean=ws_mean, sigma=ws_sigma, cov=ws_cov)

    # Run WS-CMA-ES
    print(" g    f(x1,x2)     x1      x2  ")
    print("===  ==========  ======  ======")
    while True:
        solutions = []
        for _ in range(optimizer.population_size):
            x = optimizer.ask()
            value = target_task(x[0], x[1])
            solutions.append((x, value))
            print(
                f"{optimizer.generation:3d}  {value:10.5f}"
                f"  {x[0]:6.2f}  {x[1]:6.2f}"
            )
        optimizer.tell(solutions)

        if optimizer.should_stop():
            break

The full source code is available here.

Separable CMA-ES [5]

sep-CMA-ES is an algorithm which constrains the covariance matrix to be diagonal. Due to the reduction of the number of parameters, the learning rate for the covariance matrix can be increased. Consequently, this algorithm outperforms CMA-ES on separable functions.

Source code

import numpy as np
from cmaes import SepCMA

def ellipsoid(x):
    n = len(x)
    if len(x) < 2:
        raise ValueError("dimension must be greater one")
    return sum([(1000 ** (i / (n - 1)) * x[i]) ** 2 for i in range(n)])

if __name__ == "__main__":
    dim = 40
    optimizer = SepCMA(mean=3 * np.ones(dim), sigma=2.0)
    print(" evals    f(x)")
    print("======  ==========")

    evals = 0
    while True:
        solutions = []
        for _ in range(optimizer.population_size):
            x = optimizer.ask()
            value = ellipsoid(x)
            evals += 1
            solutions.append((x, value))
            if evals % 3000 == 0:
                print(f"{evals:5d}  {value:10.5f}")
        optimizer.tell(solutions)

        if optimizer.should_stop():
            break

Full source code is available here.

IPOP-CMA-ES [6]

IPOP-CMA-ES is a method to restart CMA-ES with increasing population size like below.

visualize-ipop-cmaes-himmelblau

Source code

import math
import numpy as np
from cmaes import CMA

def ackley(x1, x2):
    # https://www.sfu.ca/~ssurjano/ackley.html
    return (
        -20 * math.exp(-0.2 * math.sqrt(0.5 * (x1 ** 2 + x2 ** 2)))
        - math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
        + math.e + 20
    )

if __name__ == "__main__":
    bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
    lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]

    mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
    sigma = 32.768 * 2 / 5  # 1/5 of the domain width
    optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)

    for generation in range(200):
        solutions = []
        for _ in range(optimizer.population_size):
            x = optimizer.ask()
            value = ackley(x[0], x[1])
            solutions.append((x, value))
            print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
        optimizer.tell(solutions)

        if optimizer.should_stop():
            # popsize multiplied by 2 (or 3) before each restart.
            popsize = optimizer.population_size * 2
            mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
            optimizer = CMA(mean=mean, sigma=sigma, population_size=popsize)
            print(f"Restart CMA-ES with popsize={popsize}")

Full source code is available here.

BIPOP-CMA-ES [7]

BIPOP-CMA-ES applies two interlaced restart strategies, one with an increasing population size and one with varying small population sizes.

visualize-bipop-cmaes-himmelblau

Source code

import math
import numpy as np
from cmaes import CMA

def ackley(x1, x2):
    # https://www.sfu.ca/~ssurjano/ackley.html
    return (
        -20 * math.exp(-0.2 * math.sqrt(0.5 * (x1 ** 2 + x2 ** 2)))
        - math.exp(0.5 * (math.cos(2 * math.pi * x1) + math.cos(2 * math.pi * x2)))
        + math.e + 20
    )

if __name__ == "__main__":
    bounds = np.array([[-32.768, 32.768], [-32.768, 32.768]])
    lower_bounds, upper_bounds = bounds[:, 0], bounds[:, 1]

    mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
    sigma = 32.768 * 2 / 5  # 1/5 of the domain width
    optimizer = CMA(mean=mean, sigma=sigma, bounds=bounds, seed=0)

    n_restarts = 0  # A small restart doesn't count in the n_restarts
    small_n_eval, large_n_eval = 0, 0
    popsize0 = optimizer.population_size
    inc_popsize = 2

    # Initial run is with "normal" population size; it is
    # the large population before first doubling, but its
    # budget accounting is the same as in case of small
    # population.
    poptype = "small"

    for generation in range(200):
        solutions = []
        for _ in range(optimizer.population_size):
            x = optimizer.ask()
            value = ackley(x[0], x[1])
            solutions.append((x, value))
            print(f"#{generation} {value} (x1={x[0]}, x2 = {x[1]})")
        optimizer.tell(solutions)

        if optimizer.should_stop():
            n_eval = optimizer.population_size * optimizer.generation
            if poptype == "small":
                small_n_eval += n_eval
            else:  # poptype == "large"
                large_n_eval += n_eval

            if small_n_eval < large_n_eval:
                poptype = "small"
                popsize_multiplier = inc_popsize ** n_restarts
                popsize = math.floor(
                    popsize0 * popsize_multiplier ** (np.random.uniform() ** 2)
                )
            else:
                poptype = "large"
                n_restarts += 1
                popsize = popsize0 * (inc_popsize ** n_restarts)

            mean = lower_bounds + (np.random.rand(2) * (upper_bounds - lower_bounds))
            optimizer = CMA(
                mean=mean,
                sigma=sigma,
                bounds=bounds,
                population_size=popsize,
            )
            print("Restart CMA-ES with popsize={} ({})".format(popsize, poptype))

Full source code is available here.

Benchmark results

Rosenbrock function	Six-Hump Camel function

This implementation (green) stands comparison with pycma (blue). See benchmark for details.

Project: cmaes

Project Details

Project Popularity

CMA-ES

News

Installation

Usage

CMA-ES variants

CMA-ES with Margin [3]

Warm Starting CMA-ES [4]

Separable CMA-ES [5]

IPOP-CMA-ES [6]

BIPOP-CMA-ES [7]

Benchmark results

Links

Related Projects